A journey in numerical linear algebra: a workshop in honor of Michele Benzi’s 60th birthday
Aula Magna
Dipartimento di Matematica, Università di Pisa
 This two-day workshop will take place in June 2022 at the Department of Mathematics of the University of Pisa, Italy, from Friday, June 10 to Saturday, June 11. It aims at bringing together experts in the field of numerical linear algebra.
This two-day workshop will take place in June 2022 at the Department of Mathematics of the University of Pisa, Italy, from Friday, June 10 to Saturday, June 11. It aims at bringing together experts in the field of numerical linear algebra.
The meeting is dedicated to the 60th birthday of Michele Benzi.
For those registered as online speaker, it will be possible to attend the meeting online.
-
-
1
Welcome remarksSpeaker: Luigi Ambrosio (Scuola Normale Superiore, Pisa)
-
2
OpeningSpeaker: Dario Bini (University of Pisa)
-
3
What makes a network "complex"?
The advent of Network Science was precipitated by an urgent need to decipher simple mechanisms that could explain the formation and growth of natural and man-made networks. The large-scale structural patterns of these networks systematically deviate from stylized models such as random networks or lattices in a variety of ways, which include the existence of phenomena like “small-worldness” (SW) and “scale-freeness” (SF) (see [1] and refs. therein).
Although these mechanisms explain some of the structural properties of real-world networks they also open intriguing questions. For instance, it is easy to see that the SW mechanism reduces mean path length simply by creating shortcuts, making enhanced connectivity overly dependent –and thus, fragile– on them. Likewise, SF-like networks are robust against random node removal but highly fragile against selected removal of highly connected nodes (hubs). It turns out that an optimal (geodesic) navigation of SW and SF networks tends on average to “overuse” both shortcuts or hubs, making these the first candidates to experience jamming, a property that induces a failure cascade which can severely harm the macroscopic network’s function.
Here we investigate the microscopic structure of SW and SF networks and discovered that both mechanisms generate topological bypasses connecting pairs of nodes, which facilitates the network communication beyond the topological shortest paths. We model the dynamics on the network by using the time-dependent Schrodinger equation with a tight-binding (TB) Hamiltonian H. Then, the real-time propagator $e^{-it \mathcal{H}/\hbar}$ is mapped into the thermal propagator $e^{−\beta \mathcal{H}}$, where $\beta$ is the inverse temperature of a thermal bath in which the network is submerged to. After setting appropriately the TB parameters we get that $\mathcal H = -A$, such that we define:
$$ \hspace{5cm} \xi_{vw}(\beta) := \langle \psi_v - \psi_w | e^{\beta A} | \psi_v - \psi_w \rangle, \hspace{5cm} (1) $$ which accounts for the <i>resistance</i> offered by the network to the displacement of the particle from the node $v$ to the node $w$ at inverse temperature $\beta$. We proved that $\xi_{vw}(\beta)$ is a square Euclidean distance between the pair of nodes $v$ and $w$ [2]. Further we define a walk-based network entropy, which accounts for the structural ordering of the network produced by the emergence of walks among pairs of nodes. Using it, we shown that both mechanisms, SW and SF, increase network entropy as a result of rocketting the choices that the particle has to navigate between every pair of nodes (see Fig. 1). Therefore, a particle navigating between a pair of nodes $v$ and $w$ can go through the topological shortest path (SP) connecting it or via some of the alternative bypasses created by the SW and SF mechanisms. We assume that the particle will “select” such a path that minimizes the thermal resistance between the two nodes. Based on $\xi_{vw}(\beta)$ we obtain the energy $\epsilon$ that a particle needs to travel between a given pair of nodes using a given path that connects them. The path for which the particle needs minimum energy among all which connect a pair of nodes is named the thermally resistive shortest paths (TRSP). We investigate when the TRSP is favored over the SP for the navigation between pairs of nodes in a network created by the Watt-Strogatz (WS) SW mechanism as well as by the Barabasi-Albert (BA) SF one. The results are illustrated in Fig. 1. We can see that the change of the net energy factor $\epsilon$ exhibits a non-monotonic shape as a function of the rewiring probability p in the so-called small-world regime. In fact, our measure detects a minimum for $p \approx 0.15$ at which, on average, traveling through the TRSP is energetically much more favorable than traveling through the SP. We call this probability the “good navigational point” (GNP) of the network, $pGNP$. This is also observed in panel (b) for the BA model. Observe that $\epsilon$ is again non-monotonic with a minimum close to $\langle k \rangle \approx 11$, i.e. BA model for which $\langle k \rangle_{GNP} \approx 11$. Finally, we show how this property influences dynamical processes (synchronization and diffusion) taken place on the networks and investigate the existence of such bypasses in several real-world networks. Therefore we conclude that:“a network is complex when its structure is sufficiently rich in walks connecting pairs of nodes as for TRSP emerge as
alternative routes that avoid SP and through-hubs navigation, which therefore increases network robustness against jamming”.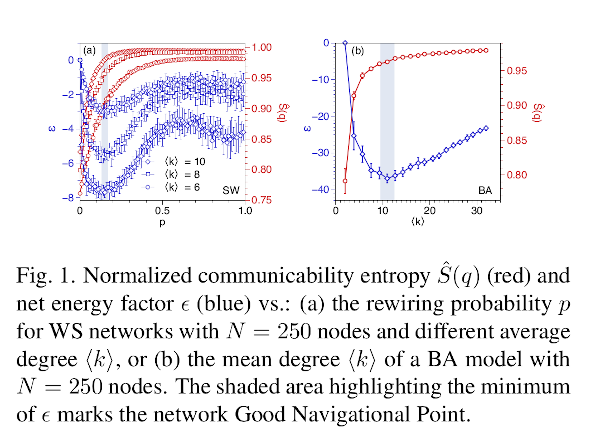
References
[1] E. Estrada, The Structure of Complex Networks. Theory and Applications (Oxford University Press, Oxford, 2011).
[2] E. Estrada, The communicability distance in graphs. Lin. Al-
gebra Appl. 436, 4317-4328 (2012)Speaker: Ernesto Estrada (Institute of Cross/Disciplinary Physics and Complex Systems, UIB-CSIC, Palma de Mallorca) -
4
Null space-based approaches for the least squares and symmetric saddle-point problems
Consider saddle-point systems of the following form
$$ \hspace{5.5cm} \mathcal{A} \left( \begin{array}{c} u \\ v \end{array} \right) = \left( \begin{array}{cc} A & B^T \\ B & 0 \\ \end{array} \right) \left( \begin{array}{c} u \\ v \end{array} \right) = \left( \begin{array}{c} f \\ g \end{array} \right) \hspace{5.5cm} (1) $$ where $A \in \mathbb{R}^{n \times n}$ is large, sparse and symmetric positive definite and $B \in \mathbb{R}^{k \times n} (n > k)$ has full rank. Such systems arise in various scientific applications, including the finite element approximation of PDEs in which a constraint is enforced on a subset of unknowns via a global scalar Lagrange multiplier, numerical continuation methods for large nonlinear systems of equations, constrained optimization as well as in linear least squares problems [2]. Null-space methods represent one of possible solution approaches to solve such systems. Despite these solution approaches that compute a null-space $Z \in \mathbb{R}^{n \times (n-k)}$ basis of the undetermined block $B$ are traditional in various engineering communities and offer advantages in some situations, general techniques to obtain such bases useful for large and sparse $A$ have not been studied frequently in the past. There are more reasons for this. One of them may be that the resulting transformed system with the matrix $Z^TAZ$ is often dense, or ill-conditioned, or both. Another reason may be that there is a lack of efficient preconditioners for the transformed systems even when the projected matrix $Z^T AZ$ is reasonably sparse. The core of the talk is devoted to discussing various algorithms to find the null-space basis $Z$. Although in several of the approaches treatment of $B$ that does not have full-rank is not difficult, we do not treat such cases at length. Initial motivation for studying the null-space approaches in this talk is slightly different from the symmetric saddle-point problem given above. Consider the linear least-squares (LS) problem $$ \min_x \| Ax - b \|_2, $$ where the system matrix $A \in \mathbb{R}^{m \times n} (m \geq n)$ and the right-hand side $b \in \mathbb{R}^m$ are given. Assume that a part of the rows of $A$ is dense and the rows have been initially permuted such that the dense rows are the last rows of $A$. If we assume a conformal partitioning of the vector $b$ we have $$ A = \left( \begin{array}{c} A_s \\ A_d \end{array} \right), \ A_s \in \mathbb{R}^{m_s \times n}, \ A_d \in \mathbb{R}^{m_d \times n}, \ b = \left( \begin{array}{c} b_s \\ b_d \end{array} \right), \ b_s \in \mathbb{R}^{m_s}, \ b_d \in \mathbb{R}^{m_d}, $$ where $m_s$ denotes the number of sparse rows of $A$, and $m_d$ is the number of dense rows, with $m = m_s + m_d$, $m_s \geq n > m_d \geq 1$ and $m_d \ll m_s$. The normal equations that describe the solution [3] (not representing always the best way to get the solution) become $$\hspace{5cm} Cx = (C_s + A^T_d A_d)x = c, \ c = A^T_s b_s + A^T_d b_d, \hspace{5cm} (2) $$ where $C_s = A^T_s A_s$ is the reduced normal matrix. The solution of (2) can be obtained from the equivalent $(n + md) \times (n + md)$ system $$ \hspace{6.3cm} \left( \begin{array}{cc} C_s & A_d^T \\ A_d & -I \\ \end{array} \right) \left( \begin{array}{c} x \\ A_d x \end{array} \right) = \left( \begin{array}{c} c \\ 0 \end{array}\right) \hspace{6.3cm} (3) $$ This is the system nearly of the form (1) with $k = m_d, H = C_s, B = A_d$. But the $(2,2)$ block is nonzero and equal to the negative unit matrix of the appropriate dimension. Provided $A_s$ has full column rank, $C_s$ is symmetric positive definite. But the null-space based approach can be extended even if the $(2, 2)$ block is nonzero and $C_s$ only positive semidefinite. This positive definiteness is quite common in the LS problems even when the whole $A$ is of full column rank. The approach to solve (3) also in this case for the full rank LS problem (3) is motivated by the following simple lemma. \textbf{Lemma}: Consider $A = A_s A_d,\ As \in \mathbb{R}^{m_s \times n}, A_d \in \mathbb{R}^{m_d \times n}$. If $A$ is of full column rank, then $C_s = A^T_s A_s$ is positive definite on the null space of $A_d$. Success of any null-space approach then depends on constructing a suitable null-space basis that keeps the matrix $Z^T AZ$ sufficiently sparse and well-conditioned. Of course, it cannot be an orthogonal null-space basis computed, for example, by pivoted $QR$ factorization of $B^T$. We will discuss other approaches to find the null-space basis heavily based on the fact that $B$ is wide. That is, it has far fewer rows than columns. The approaches include computing an oblique basis $Z$ computed from more separate QR factorizations and an approach that adds rows of $B$ one by one and extends the basis incrementally. Another approach for constructing $Z$ is the right oblique conjugation. Applied to $B \in \mathbb{R}^{k \times n}$ it yields $V \in \mathbb{R}^{n \times n}$ and lower trapezoidal $L \in \mathbb{R}^{k \times n}$ satisfying $$ \hspace{8cm} BV = L. \hspace{8cm} (4) $$The null-space basis is then formed by the last $n-k$ columns of $V$ . This approach is directly related to Thesis of Michele Benzi [1]. Techniques implied by this Thesis have motivated the right oblique conjugation, and they may still offer further computational possibilities. Not only for constructing $Z$ but possibly also for preconditioning of the linear systems with the matrix $Z^T AZ$.Our experimental results show that the null-space bases obtained from the mentioned approaches are of high quality and can push forward further research in optimization and solving constrained least squares. Linear least squares problems that contain a small number of dense rows arising from practical applications are used to illustrate our ideas and to explore their potential for solving large-scale systems. Our work was originally motivated by the paper by Howell [4]. A significant part of the obtained results has been published in [5].
References
[1] M. Benzi, A Direct Row-Projection Method For Sparse Linear Systems, Ph.D. Thesis, NCSU, 1993.
[2] M. Benzi, G.H. Golub, and J. Liesen, Numerical solution of saddle point problems, Acta Numerica,
14:1–137, 2005.
[3] ̊A. Bj ̈orck, Numerical Methods for Least Squares Problems, SIAM, Philadelphia, 1996.
[4] J. S. Howell, Prestructuring sparse matrices with dense rows and columns via null space methods,
Numerical Linear Algebra with Applications, 25:1–30, 2018.
[5] J. A. Scott and M. T ̊uma, A null-space approach for large-scale symmetric saddle point systems with
a small and non zero (2,2) block, Numerical Algorithms, published online, 2022.Speaker: Miroslav Tůma (Charles University) -
5
Rational Krylov subspaces for Hermitian matrices: properties and applications
Rational Krylov subspaces have become a fundamental ingredient in numerical linear algebra methods associated with reduction strategies. Nonetheless, a lot of their potential is still to be explored.
In particular, many structural properties of the reduced matrices in these subspaces are not fully understood. We advance in this analysis by deriving decay bounds on the entries of rational Krylov reduced matrices and of their functions, which hold in spite of the lack of any banded structure in the considered matrices.
Moreover, when data matrices are Hermitian, a short-term recurrence can be used to generate an associated orthonormal basis. We propose an implementation that allows one to obtain the rational subspace reduced matrices at lower overall computational costs than proposed in the literature. Applications are discussed where the short-term recurrence feature can be exploited to avoid storing the whole orthonormal basis.
This presentation is based on joint works with Davide Palitta, Università di Bologna, and Stefano Pozza, Charles University, Prague.
Speaker: Valeria Simoncini (Università di Bologna) -
16:30
Coffee break
-
6
Computing the Square Root of a Low-Rank Perturbation of the Scaled Identity Matrix
We consider the problem of computing the square root of a perturbation of the scaled identity matrix, $A = \alpha I_n + UV^{*}$, where $U$ and $V$ are $n \times k$ matrices with $k \leq n$.
This problem arises in various applications, including computer vision and optimization methods for machine learning. We derive a new formula for the pth root of $A$ that involves a weighted sum of powers of the pth root of the $k \times k$ matrix $\alpha I_k + V^*U$. This formula is particularly attractive for the square root, since the sum has just one term when $p = 2$. We also derive a new class of Newton iterations for computing the square root that exploit the low-rank structure. We test these new methods on random matrices and on positive definite matrices arising in applications. Numerical experiments show that the new approaches can yield much smaller residual than existing alternatives and can be significantly faster when the perturbation $UV^*$ has low rank.
This is joint work with Massimiliano Fasi and Xiaobo Liu.
Speaker: Nick Higham (University of Manchester) -
7
Reduced-Order Models for Parametrized PDE Models with Constraints
Various phenomena simulated using partial differential equations (PDEs) give rise to constrained systems of equations. These include models of optimal control with constraints given by elliptic PDEs, as well as fundamental models of fluid dynamics such as the Stokes equations where the constraints correspond to the incompressibility (divergence-free) condition. If these models also depend on random (parametrized) input data, than it is important to develop reduced-order models (ROMs) to reduce the computational costs associated with multiple solutions of the large-scale algebraic systems that arise from discretization. Several approaches have been developed to construct ROMs for constrained problems. These approaches supplement greedy search strategies [4] with methods that augment the spaces obtained from searching in order to enforce inf-sup stability, which otherwise does not hold in the reduced spaces. In this work, we present two sets of results. The first is a comparison of the effectiveness of two such methods for augmentation, known as aggregation methods [3] and supremizing methods [1, 2]. The second is an introduction of a new approach that avoids the difficulties caused by lack of inf-sup stabiity by forcing the reduced model to have a simpler structure not of saddle-point form.
References
[1] A. Quarteroni and G. Rozza, Numerical solution of parametrized Navier-Stokes equations by reduced basis methods, Numerical Methods for Partial Differential Equations 23(4):923–948, 2007.
[2] G. Rozza and K. Veroy, On the stability of the reduced basis method for Stokes equations in parametrized domains, Computer Methods in Applied Mechanics and Engineering 196(7):1244–1260, 2007.
[3] F. Negri and G. Rozza and A. Manzoni and A. Quarteroni, Reduced basis method for parametrized optimal control problems, SIAM Journal on Scientific Computing 35(5): A2316-A2340, 2013
[4] A. Buffa, Y. Maday, A. T. Patera, C. Prud’homme, and G. Turinici. A priori convergence of the greedy algorithm for the parametrized reduced basis method ESAIM: Mathematical Modelling and Numerical Analysis 46(03):595–603, 2012.Speaker: Howard Elman (University of Maryland at College Park) -
8
Towards Resilient and Robust Asynchronous Linear Systems Solvers for Edge Computing
Wearable healthcare devices, content delivery systems, and smart home devices are pushing applications, data, services and, consequently, large-scale computations away from centralized environments onto the network, closer to the requests. Newly emerging technology of edge computing, where networked, autonomous devices work collaboratively to achieve a common goal through the synergy of humans and machines, requires asynchronous, flexible and resilient algorithms for decentralized processing, communication and predictions in heterogeneous environments. While the benefits of developing autonomous capabilities are multifold, edge computing systems are subject to device failures, partial data losses, or security attacks, and hence require multidimensional resilience solutions. In this talk, we will present our recently developed resilience and robustness improvements when solving linear systems of equations with asynchronous Jacobi
(ASJ) method. Inspired by the ADMM (Alternating Direction Method of Multipliers) and average consensus push-sum, we derived rejection and update criteria that allow to restore the convergence of the original ASJ method in the presence of data corruption or communication delays.Speaker: Agnieszka Miedlar (University of Kansas) -
9
Anderson acceleration with approximate least-squares calculations: applications to scientific computing
We provide rigorous theoretical bounds for Anderson acceleration (AA) that allow efficient approximate calculations of the residual that reduce communication time and storage space while maintaining convergence. Specifically, we propose a reduced variant of AA, which consists in projecting the least squares to compute the Anderson mixing onto a subspace of reduced dimension. We numerically assess the performance of the reduced AA on: (i) linear deterministic fixed-point iterations arising from the Richardson’s scheme to solve linear systems with open-source benchmark matrices with various preconditioners, (ii) non-linear deterministic fixed-point iterations arising from non-linear time-dependent Boltzmann equations, and (iii) non-linear stochastic fixed-point iterations arising from the training of neural networks. The dimensionality of the subspace onto which the least-squares to compute AA is projected adapts dynamically at each iteration as prescribed by computable quantities derived from the theoretical error bounds. The results show a reduction of the computational time without compromising the final accuracy.
This work was supported in part by the Office of Science of the Department of Energy, by the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the U.S. Department of Energy Office of Science and the National Nuclear Security Administration, and by the Laboratory Directed Research and Development (LDRD) Program of Oak Ridge National Laboratory managed by UT-Battelle, LLC for the US Department of Energy under contract DE-AC05-00OR22725. This work used resources of the Oak Ridge Leadership Computing Facility and of the Edge Computing program at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725.References
[1] D. G. Anderson, Iterative procedures for nonlinear integral equations, Journal of the Association for Computing Machinery, 12(4), 1965.
[2] V. Simoncini and D. Szyld, Theory of inexact Krylov subspace methods and applications to scientific computing, SIAM Journal on Scientific Computing, 25(2), pp. 454–477, 2003.
[3] H. F. Walker and P. Ni, Anderson acceleration for fixed-point iterations, SIAM Journal on Numerical Analysis, 49(4), pp. 1715–1735, 2011.
[4] A. Toth and C. T. Kelley, Convergence analysis for Anderson acceleration, SIAM Journal on Numerical Analysis, 53(2), pp. 805–819, 2015.
[5] C. Brezinski, M. Redivo-Zaglia and Y. Saad, Shanks sequence transformations and Anderson acceleration, SIAM Review, 60(3), 2018,
[6] M. Lupo Pasini, Convergence analysis of Anderson-type acceleration of Richardson’s iteration, Numerical Linear Algebra with Applications, 26(4), 2019.
[7] C. Brezinski, S. Cipolla, M. Redivo-Zaglia and Y. Saad, Shanks and Anderson-type acceleration techniques for systems of nonlinear equations, IMA Journal of Numerical Analysis, drab061, https://doi.org/10.1093/imanum/drab061, 2021.Speaker: Lupo Pasini Massimiliano (Oak Ridge National Laboratory)
-
1
-
-
10
Differential-algebraic systems with symmetry structures
Linear time-varying differential-algebraic equations with extra symmetries such as self-adjoint and skew-adjoint systems are studied. Local and global canonical forms under congruence are presented and used to classify the geometric properties of the flow associated with the differential equation as symplectic or generalized orthogonal flow. As applications, the results are applied to the analysis of dissipative Hamiltonian systems arising from circuit simulation and incompressible flow.
Joint work with Peter Kunkel.
Speaker: Volker Mehrmann (TU Berlin) -
11
On non-Hermitian positive (semi)definite linear algebraic systems arising from dHDAE systems
It is well known that every matrix $A \in \mathbb{C}^{n \times n}$ can be split into its Hermitian and skew-Hermitian parts, i.e.,
$$A = H + S, \quad H = \frac{1}{2}(A + A^*), \quad S = \frac{1}{2}(A - A^*),$$ so that $H = H^{*}$ and $S=-S^{*}$. This simple, yet fundamental observation has many applications. For example, Householder used it in The Theory of Matrices (1964) to show that all eigenvalues of $A = H + S$ lie in or on the smallest rectangle with sides parallel to the real and imaginary axes that contains all eigenvalues of $H$ and of $S$. This result, attributed to Bendixson (1902), is very useful in the analysis of spectral properties of saddle point matrices; see, e.g., [1, Section 3.4] or [2]. It implies that if $H$ is positive definite, then all eigenvalues of $A$ have a positive real part. Therefore such (in general non-Hermitian) matrices A are sometimes called positive real or positive stable, but we call $A = H + S$ positive (semi)definite if $H$ has the corresponding property. In the first part of this talk we will discuss an important class of practically relevant applications where the splitting $A = H + S$ occurs naturally and has a physical meaning. These applications arise from energy-based modeling using differential algebraic equation (DAE) systems in dissipative Hamiltonian (dH) form, or shortly dHDAE systems. The usefulness and applicability of this modeling approach has been demonstrated in a variety of application areas such as thermodynamics, electromagnetics, fluid mechanics, chemical processes, and general optimization.In the second part we will study the linear algebraic systems arising in this context, and their solution by Krylov subspace methods. The (non-Hermitian) matrices A that occur are positive definite or positive semidefinite. In the positive definite case we can solve the linear algebraic systems using Krylov subspace methods based on efficient three-term recurrences. Such methods were already derived by Widlund [6] (based on earlier work of Concus and Golub [3]) and Rapoport [5]
in the late 1970s. These methods are not widely used or known, and we will therefore summarize the most important facts about their implementation and their mathematical properties. The semidefinite case can be challenging and requires additional techniques to identify and deal with
the “singular part” of the matrix, while the “positive definite part” can still be treated with the three-term recurrence methods. We will illustrate the performance of the iterative methods and compare them with (preconditioned) GMRES on several computed examples.The talk is based on joint work with Candan Güdücü, Volker Mehrmann, and Daniel B. Szyld [4].
References
[1] M. Benzi, G. H. Golub and J. Liesen, Numerical solution of saddle point problems Acta Numer., 14
(2005), pp. 1–137.
[2] M. Benzi and V. Simoncini, On the eigenvalues of a class of saddle point matrices, Numer. Math., 103
(2006), pp. 173–196.
[3] P. Concus and G. H. Golub, A generalized conjugate gradient method for nonsymmetric systems of
linear equations, in Computing methods in applied sciences and engineering (Second Internat. Sympos.,
Versailles, 1975), Part 1, Roland Glowinski and Jaques-Louis Lions, eds., vol. 134 of Lecture Notes in
Econom. and Math. Systems, Springer, Berlin, 1976, pp. 56–65.
[4] C. Güdücü, J. Liesen, V. Mehrmann, and D. B. Szyld, On non-Hermitian positive (semi)definite linear
algebraic systems arising from dissipative Hamiltonian DAEs, arXiv:2111.05616, 2021.
[5] D. Rapoport, A Nonlinear Lanczos Algorithm and the Stationary Navier-Stokes Equation, PhD thesis,
Department of Mathematics, Courant Institute, New York University, 1978.
[6] O. Widlund, A Lanczos method for a class of nonsymmetric systems of linear equations, SIAM J.
Numer. Anal., 15 (1978), pp. 801–812.Speaker: Jörg Liesen (TU Berlin) -
12
Provable convergence rate for asynchronous methods via randomized linear algebra
Asynchronous methods refer to parallel iterative procedures where each process performs its task without waiting for other processes to be completed, i.e., with whatever information it has locally available and with no synchronizations with other processes. For the numerical solution of a general partial differential equation on a domain, Schwarz iterative methods use a decomposition of the domain into two or more (usually overlapping) subdomains. In essence one is introducing
new artificial boundary conditions Thus each process corresponds to a local solve with boundary conditions from the values in the neighboring subdomains.Using this method as a solver, avoids the pitfall of synchronization required by the inner products in Krylov subspace methods. A scalable method results with either optimized Schwarz or when a coarse grid is added. Numerical results are presented on large three-dimensional problems illustrating the efficiency of asynchronous parallel implementations.
Most theorems show convergence of the asynchronous methods, but not a rate of convergence. In this talk, using the concepts of randomized linear algebra, we present provable convergence rate for the methods for a class of nonsymmetric linear systems. A key element in the new results is the choice of norm for which we can prove convergence of the residual in the expected value sense.
Speaker: Daniel Szyld (Temple University) -
13
Improved parallel-in-time integration via low-rank updates and interpolation
This talk is concerned with linear matrix equations that arise from the space-time discretization of time-dependent linear partial differential equations (PDEs). Such matrix equations have been considered, for example, in the context of parallel-in-time integration leading to a class of algorithms called ParaDiag, see [1] and the references therein. In this talk, we describe and analyze two novel approaches for the numerical solution of such equations. Our first approach is based on the
observation that the modification of these equations performed by ParaDiag in order to solve them in parallel has low rank. Building upon previous work on low-rank updates of matrix equations [2], this allows us to make use of tensorized Krylov subspace methods or the techniques from [4] to account for the modification. Our second approach is based on
interpolating the solution of the matrix equation from the solutions of several modifications. Both approaches avoid the use of iterative refinement needed by ParaDiag and related space-time approaches [3] in order to attain good accuracy. In turn, our new approaches have the potential to outperform, sometimes significantly, existing approaches. This potential is demonstrated for several different types of PDEs.References
[1] M. J. Gander, J. Liu, S.-L. Wu, X. Yue, and T. Zhou. ParaDiag: parallel-in-time algorithms based on the diagonalization technique. arXiv preprint arXiv:2005.09158, 2020.
[2] D. Kressner, S. Massei, and L. Robol. Low-rank updates and a divide-and-conquer method for linear matrix equations. SIAM J. Sci. Comput., 41(2):A848–A876, 2019.
[3] E. McDonald, J. Pestana, and A. Wathen. Preconditioning and iterative solution of all-at-once systems for evolutionary partial differential equations. SIAM J. Sci. Comput., 40(2):A1012–A1033, 2018.
[4] D. Palitta. Matrix equation techniques for certain evolutionary partial differential equations. J. Sci. Comput., 87(3):Paper No. 99, 36, 2021.Speaker: Daniel Kressner (EPFL) -
10:45
Coffee break
-
14
Augmented Lagrangian preconditioner for fluids on surfaces
Augmented Lagrangian preconditioner for linearized incompressible Navier-Stokes equations has
been introduced in [1,2]. Over the years it was proved to be an efficient technique to solve highly
non-symmetric algebraic systems having a saddle point structure and resulting from discretizations
of fluid problems. In the talk we review the approach and discuss some of its recent developments.
In particular, we introduce the Augmented Lagrangian preconditioner for the algebraic systems of
unfitted finite element discretizations of fluid equations posed on smooth closed surfaces. A matrix
of the system features a sign-indefinite (2,2)-diagonal block with a high-dimensional kernel that
requires special handling. We further consider a reuse of matrix factorization as a building block
in the full and modified Augmented Lagrangian preconditioners. The strategy, applied to solve
two-dimensional incompressible fluid problems, yields efficiency rates independent of the Reynolds
number. The talk partially covers results from [3].References
[1] M. Benzi and M. Olshanskii, An augmented Lagrangian approach to linearized problems in hydrodynamic
stability, SIAM J. Sci. Comp. 30 (2005), pp. 1459–1473.
[2] M. Benzi, M. Olshanskii, Z. Wang, Modified augmented Lagrangian preconditioners for the incom-
pressible Navier-Stokes equations, Int. J. Numer. Meth. Fluids 66 (2011), pp. 486–508.
[3] M. Olshanskii and A. Zhiliakov, Recycling augmented Lagrangian preconditioner in an incompressible
fluid solver, Numerical Linear Algebra with Applications 29 (2022), e2415.Speaker: Maxim Olshanskii (Department of Mathematics, University of Houston) -
15
Computing the most stable switching laws of a linear system.
When considering the stability under arbitrary switching of a discrete-time linear switched system
$$ x(n + 1) = A_{\sigma(n)} x(n), \qquad \sigma : \mathbb N \to \left\{ 1, . . . , m \right\}, $$ where $x(0) \in \mathbb{R}^d$, the matrix $A_{\sigma(n)} \in \mathbb{R}^{d \times d}$ belongs to a finite family $F = \{ A_i \}_{1 \leq i \leq m}$ and $\sigma$ denotes the switching law, it is known that the most stable switching laws are associated to the so-called spectrum-minimizing products of the family $F$. The minimal rate of growth of its trajectories is called lower spectral radius and is denoted as $\hat \rho(F)$. For a normalized family $F$ of matrices (i.e., with lower spectral radius $\hat \rho(F) = 1$) that share an invariant cone $K$ (the most typical case is the positive orthant for nonnegative matrices), all the most stable trajectories starting from the interior of $K$ lie on the boundary of a certain invariant set (called Barabanov antinorm), for which a canonical constructive procedure is available [4], that is based on the invariant polytope algorithm developed in [3]. After presenting the main results for this case, I will consider families of matrices $F$ that share an invariant multicone $K_{\mathrm{mul}}$ [1, 2] and show how to generalize some of the known results to this more general setting (Guglielmi & Zennaro, in progress [5]). These generalizations are of interest because common invariant multicones may well exist when common invariant cones do not.References
[1] M. Brundu, M. Zennaro Multicones, duality and matrix invariance, J. Convex Anal. 26 (2019), pp. 1021–1052.
[2] M. Brundu, M. Zennaro Invariant multicones for families of matrices, Ann. Mat. Pur. Appl. 198 (2019), 571–614.
[3] N. Guglielmi, V.Yu. Protasov, Exact computation of joint spectral characteristics of linear operators, Found. Comput. Math., 13 (2013), pp. 37–97.
[4] N. Guglielmi, M. Zennaro Canonical construction of polytope Barabanov norms and antinorms for sets of matrices, SIAM J. Matrix Anal. Appl. 36 (2015), pp. 634–655.
[5] N. Guglielmi, M. Zennaro Antinorms for sets of matrices sharing an invariant multicone, in preparation (2022).Speaker: Nicola Guglielmi (Gran Sasso Science Institute) -
16
Preconditioned Iterative Methods for Weighted Toeplitz Least Squares Problems
In this talk we consider the problem of finding effective preconditioners for linear systems of the form $Hx = y$ where
$$ H = A^T D A + \lambda^2 L^T L $$ where $A$ and $L$ are structured matrices (e.g., Toeplitz), $D$ is a diagonal matrix, and $\lambda$ is a scalar. These linear systems can arise when iteratively computing approximations to nonlinear inverse problems. Typically in these applications the matrix $D$ changes at each nonlinear iteration, but $A$ and $L$ remain constant. Benzi and Ng [1] considered linear systems of this form, and proposed an effective variant of constraint preconditioning and a Hermitian/skew-Hermitian splitting (HSS) preconditioner. In this talk we consider an alternative approach based on low-rank matrix approximations.References
[1] M. Benzi, M. K. Ng Preconditioned Iterative Methods for Weighted Toeplitz Least Squares Problems SIAM J. Matrix Anal. Appl., 27 (2006), pp. 1106–1124.
Speaker: James Nagy (Department of Mathematics, Emory University) -
17
Restarts for matrix Laplace transforms
Let $A \in \mathbb{C}^{n \times n}$ be a matrix, $v \in \mathbb{C}^n$ a vector, and $f: D \subseteq \mathbb{C} \to \mathbb{C}$ a function defined on the spectrum of $A$. We consider the task of computing $f(A)v$, the action of the matrix function $f(A)$ on the vector $v$. This task arises in many applications and it is a viable alternative to computing $f(A)$ directly, which is impossible if $A$ is large and sparse.
In this talk we consider the Arnoldi approximation, a Krylov subspace extraction for $f(A)v$. Since a new vector needs to be generated and stored in every iteration, one is often forced to rely on restart algorithms which are either not efficient or not stable or only applicable to restricted classes of functions. This holds already to some extent in the symmetric case, because of storage restrictions, and is very prominent in the non-symmetric case due to the increasing cost of orthogonalizations.
We present a new representation of the error of the Arnoldi iterates if the matrix function $f$ can be represented as a Laplace transform
$$ f(t) = \int_0^\infty g(s) e^{-st}\ ds, $$ and develop a restarted algorithm for computng $f(A)v$ based on this error representation. The error representation uses a long known error representation for $exp(-tA)v$, and it generalizes earlier work of some of the authors on quadrature-based restarts for Stieltjes matrix functions. The error representations involve iterated Laplace transform, so that particular care must be taken on how to devise efficient quadrature rules. We do so by using, in particular, spline interpolation.We will present several numerical experiments illustrating the efficieny of our approach, including fractional diffusion on graphs and the matrix Gamma function.
Speaker: Andreas Frommer (Bergische Universitaet Wuppertal) -
13:15
Light lunch
-
10
